Introductiontothephenomenon
Thelightintensitydistributiongeneratedwhenseverallightwaves(memberwaves)meetisnotequaltothesumofthelightintensitydistributioncausedbyeachmemberwavealone,butaphenomenonoflightanddarkphasesappears..Forexample,inYoung’sdoubleholeinterference(seeYoung’sinterferenceexperiment),thewaveletfromeachsmallholeH1orH2isamemberwave.Whentheholeisverysmall,thelightintensitycausedbythememberwavefromholeH1aloneThedistributionI1(x)isroughlyuniforminarelativelylargerange;thesameistrueforthelightintensitydistributionI2(x)causedbythememberwavescomingoutoftheholeH2alone.Thesumofthetwoisstillroughlyevenlydistributed.ThelightintensitydistributionI(x)causedbythetwomemberwavestogetherhasasignificantchangeinbrightnessanddarknesswithpositionx,whichisobviouslynotequaltoI1(x)+l2(x).
Eachmemberwavealonecreatesaroughlyuniformlightintensitydistribution,whichisequivalenttorequiringnoobviousdiffractionofeachmemberwaveitself,becausediffractionwillalsocauselightanddarkfringes(seelightdiffraction).Therefore,whenseveralmemberwavesmeetandinterfereinacertainareaofspace,itshouldmeanthatthediffractionofeachmemberwavecanbeignoredinthatarea.
Itshouldbenotedthatthelightintensitymentionedaboveisnottheinstantaneousvalueofthelightfieldintensity(proportionaltothesquareoftheamplitude),buttheaverageorintegratedvalueofthelightfieldintensitywithinacertainperiodoftimeΔt;ThelengthofΔtdependsontheperformanceofthedetectionmeansordevice.Forexample,whenthehumaneyeobserves,Δtisthedurationofvision;whenshootingwithfilm,Δtistheexposuretime.
Interferencephenomenonisusuallymanifestedasafairlystablelightanddarkfringedistributionoflightfieldintensityinspace;sometimesitismanifestedaswhenacertainparameteroftheinterferencedevicechangeswithtime,receivingatafixedpointThereceivedlightintensitychangesalternatelyaccordingtoacertainrule.
Thediscoveryoflightinterferencehasplayedanindelibleroleintheevolutionofthetheoryoflightwavesfromlightparticlestolightwavesinhistory.In1801,T.Yangproposedtheprincipleofinterferenceandfirstmadeadouble-slitinterferenceexperiment.Atthesametime,healsoexplainedthecolorformedbythefilm.In1811,D.F.J.Aragofirststudiedtheinterferencephenomenonofpolarizedlight.Inmoderntimes,lightinterferencehasbeenwidelyusedinmanyfieldssuchasprecisionmetrology,astronomicalobservation,photoelasticstressanalysis,andautomaticcontrolinopticalprecisionmachining.
Productionconditions
Overview
Onlytwocoherentlightsourceswiththesamefrequency,constantphasedifferenceandthesamevibrationdirectioncanproducelightinterference.Thelightemittedbytwoordinaryindependentlightsourcescannothavethesamefrequency,letaloneafixedphasedifference,andtherefore,nointerferencephenomenoncanoccur.
Specificmethod
InordertomakethelightintensitydistributionofthesyntheticwavefieldstablewithinaperiodoftimeintervalΔt,therequirementsare:①Thefrequencyofeachmemberwavev(thereforethewavelengthλ)isthesame;②TheinitialphasedifferenceofanytwomemberwavesremainsunchangedwithinΔt.Condition②meansthatseverallightsourcesthatusuallyemitlightindependently,eveniftheyemitlightofthesamefrequency,therewillbenointerferencewhentheselightsmeet.Thereasonis:usuallythelightemittedbythelightsourceisalargenumberofwavetrainsrandomlydistributedintheinitialphase,andthedurationofeachwavetraindoesnotexceedtheorderof10seconds,thatis,every10secondsorso,theinitialphaseofthewavemustbeArandomchange.Moreover,theinitialphasesofthewavetrainsemittedbyanytwoindependentlightsourcesarestatisticallyirrelevant.Itcanbeimaginedthatwhenthewavesemittedbytheseindependentlightsourcesmeet,adefinitepatternoffringesisonlyproducedinaveryshorttime,andevery10secondsorso,itisreplacedwithanotherpattern.Sofar,therehasbeennodetection.Ortherecordingdevicecankeepupwithsuchasharpchange,sowhatisobservedistheaverageeffectoftheabove-mentionedlargenumberofpatterns,thatis,auniformlightintensitydistributionratherthanastreakoflightanddark.However,modernspeciallasershavebeenabletoemitwavetrainsaslongastensofkilometers,thatis,thewavetraindurationisontheorderof10seconds.Therefore,itcanbesaidthatifadetectorwithatimeresolutionΔtshorterthan10secondsisused(suchadevicecanbedone),thelightwavesemittedbytwoindependentlasersofthesamefrequencywillbeInterferencecanalsobeobserved.Inaddition,takingthedouble-waveinterferenceasanexample,itisalsorequired:③Theamplitudeofthetwowavesmustnotbeverydifferent;④Thepolarizationplanesofthetwowavesmustberoughlythesameatthesuperpositionpoint.
Whenthecondition③isnotsatisfied,althoughinterferencefringescanstillbeproducedinprinciple,thedifferencebetweenthelightanddarkofthefringesisverysmall,andtheinterferencephenomenonisnotobvious.Condition④Therequirementisnecessarybecausewhenthepolarizationplanesoftwolightwavesareperpendiculartoeachother,regardlessofthefixedphasedifferencebetweenthetwolightwaves,thelightintensityofthecombinedfieldisthesamevalue,andtherewillbenoalternatinglightanddark(toobserveAlternatelightanddark,withthehelpofpolarizingelements).
Theabovefourpointsarecommonlyreferredtoascoherenceconditions.Twoormorelightsourcesorlightwavesthatmeettheseconditionsarecalledcoherentlightsourcesorcoherentlightwaves.
Generatecoherentlightwaves
Overview
Thewaytoobtainasetofcoherentlightwavesfromagenerallightsourceistocombinealightsourcewithacertainopticaldevice(interferencedevice)Theemittedlightwave(sourcewave)isdividedintoseveralwaves.Sincethesewavescomefromthesamesourcewave,whentheinitialphaseofthesourcewavechanges,theinitialphaseofeachmemberwavechangesaccordingly,sothatthephasedifferencebetweenthemremainsunchanged.Atthesametime,thepolarizationdirectionofeachmemberwaveisalsoconsistentwiththesourcewave,sotheirpolarizationdirectionsarealsoroughlythesameatthepointofinvestigation.Thegeneralinterferencedevicecanmaketheamplitudeofeachmemberwavenottoogreat.Therefore,whenthelightsourceemitslightofasinglefrequency,alltheabovefourconditionscanbemet,andinterferencephenomenonoccurs.Whenthelightsourceemitsmanyfrequencycomponents,eachsingle-frequencycomponent(correspondingtoacertaincolor)willproduceacorrespondingsetoffringes,andwhenthesefringesoverlap,theywillappearascoloredfringes.
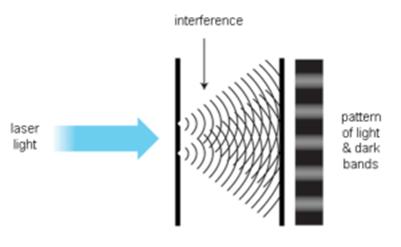
HereisasupplementtoThomasYoung’smethodofobtainingcoherentlightbackthen:byaddingasmallholeSbeforethedoublehole,accordingtoHuygensprinciple,thelightdiffractedbythesmallholeSbecomesasphericalwave,thusObtaincoherentlight.Generally,alaserwithgoodcoherenceisusedforexperiments,andthesmallholeSisnotneeded,andtheinterferencepatterncanbeobtainedbydirectlyirradiatingthelaseronthedoublehole.
Thepartialwavefrontmethod
Thepartialwavefrontmethod.Dividethewavefrontofthepointlightsourceintotwoparts,makethempassthroughtwoopticaltoolgroups,andoverlapafterbeingreflected,refractedordiffractedtoforminterferenceinacertainarea.Sinceanypartofthewavefrontcanberegardedasanewlightsource,andeachpartofthesamewavefronthasthesamephase,theseseparatedpartsofthewavefrontcanbeusedaslightsourceswiththesameinitialphase,regardlessofthephasechangeofthepointlightsourceHowfast,theinitialphasedifferenceoftheselightsourcesisconstant.Young'sdoubleslits,Fresneldouble-sidedmirrors,andLoemirrorsareallsuchwavedivisionfrontinterferencedevices.
Sub-amplitudemethod
Sub-amplitudemethod.Whenabeamoflightisprojectedontheinterfacebetweentwotransparentmedia,partofthelightenergyisreflectedandtheotherpartisrefracted.Thismethodiscalledthesub-amplitudemethod.Thesimplestamplitude-dividedinterferencedeviceisathinfilm,whichusestheupperandlowersurfacesofthetransparentfilmtosequentiallyreflectincidentlight,andtheinterferencephenomenonformedbytheencounterofthesereflectedlightwavesinspace.Sincethereflectedlightontheupperandlowersurfacesofthefilmcomesfromtwopartsofthesameincidentlight,theyonlyexperiencedifferentpathsandhaveaconstantphasedifference,sotheyarecoherentlight.Anotherimportantsub-amplitudeinterferencedeviceistheMichelsoninterferometer.
Interferencefringes
Amongallkindsofinterferencefringes,equal-inclinationinterferencefringesandequal-thicknessinterferencefringesaretwotypicalones.Theaboveassumesthatthelightsourceemitsmonochromaticlight(orafilterisusedtoextractacertainmonochromaticlightfromthelightofmanywavelengthsemittedbythelightsource).Whenthelightofmanywavelengthsemittedbythelightsourceinterferes,coloredinterferencefringes(seewhitelightfringes)areformed.
Interferenceclassification
Doublelightwaveinterference
Itistheinterferenceoftwomemberwaves.Young’sdouble-holeanddouble-slitinterference,Fresneldouble-mirrorinterferenceinvolvingNewton’srings,etc.belongtothiscategory.Thelightanddarkfringesformedbydoublelightwaveinterferencearenotsharp,butthelightintensitydistributionchangessinusoidally.Thisisthecharacteristicofdoublelightwaveinterference.Multi-waveinterferencecanformfineandsharpfringes.
Multi-waveinterference
Theinterferenceofmorethantwomemberwaves.Lumo-Gerkefilminterferencefallsintothiscategory.InFigure1,AisaparallelplateglasswithaninclinedincidentwindowBCatoneend.ThesourcewaveemittedfromSenterstheglasssheetthroughBCandisreflectedmultipletimesbetweenitsupperandlowersurfaces.Everytimeitreflectsontheuppersurface,awaveisrefractedintotheairatthesametime.Allwavesthatarerefractedintotheaireachtimeareagroupofmemberwavescausedbythesamesourcewaveinawayofsub-amplitude.ObservetheinterferencefringesonthefocalplaneΠofthelensL.ThephasedifferencebetweentwoadjacentwavesatpointPis:whereλisthewavelengthofthelightwaveinvacuum,nistherefractiveindexoftheglass,tisthethicknessoftheglasssheet,andβisthedifferencebetweentheopticalpathauxiliarylineintheglasssheetandthesurfacenormalAngle.Thefringesofthelightintensitydistributiononthereceivingsurfaceareveryfineandsharp,whichisacharacteristicofmulti-waveinterference.
Interferenceofpolarizedlight
Intheinterferencementionedabove,eachmemberwavecanbeconsideredtohavethesamepolarizationdirectionattheinspectionpoint.Whenthepolarizationplanesofthetwomemberwavesinvolvedintheinterferencesandwichacertainangle(forexample,90°),howtoproduceinterferenceistheinterferenceofpolarizedlight.
Application
Accordingtotheprincipleoflightinterference,thelengthcanbepreciselymeasured.Forexample,useMichelsoninterferometertocalibratethelengthoftheblockgauge.Themethodisasfollows.Usealaserbeamwithgoodmonochromaticity(wavelengthλ)asthelightsource,andinstallaprecisecontactonthemovablearmoftheMichelsoninterferometer,firstmakethecontactcontactoneendoftheblockgauge,Thenremovetheblockruleandmakethemovablemirrormove.Atthistime,everytimeyoumoveλ/2,theopticalpathdifferenceinthetwoarmsincreasesbyλ,sothatthedetectorplacedinthecenteroftheinterferencefieldofviewoutputsachangeinstrength,increasingthenumberofthecounterby1.Untilthecontactcontactsthebasesurface(theotherendoftheblockgaugewasoriginallyplacedonthebasesurface).Ifthetotalnumberofcountersaddedisn,thelengthoftheblockgaugeismeasured.
Theprecisedevicecanaccuratelymeasurentolessthan±0.1,sotheerrorofmeasuringlengthdoesnotexceed±λ/20.
Usinginterferencephenomenoncanalsodetecttheslightdifferencebetweenthegeometryoftheworkpiecesurfaceandthedesignrequirementsduringthemachiningprocess.Forexample,ifyouwanttoprocessaplane,youcanfirstuseprecisiontechnologytomanufactureaplaneglassplate(model)withhighprecision.Theplaneofthetemplateisbroughtintocontactwiththesurfaceoftheparttobetested,soanairfilmisformedbetweenthetwosurfaces.Ifthesurfacetobemeasuredisindeedagoodplane,theairfilmisofequalthicknesseverywhereoraregularwedgeshape.Whenlightisirradiated,theinterferencelightintensityformedbythethinfilmisapieceofuniformorparallelandevenlyspacedstraightstripes.Ifthesurfacetobemeasureddeviatesfromtheplaneinsomeareas,theintensityoftheinterferencelighthereisdifferentfromelsewhereortheinterferencefringesappeartobecurvedthere.Fromthefringevariation,itcanbeinferredthatthesurfacetobemeasureddeviatesfromtheplane.Itiseasytoobservethatthedeviationisafractionofthewavelength.
Description
①Iftheintensityofeachplaceintheoverlappingareaisnotexactlythesame,acertainintensitydistributionisformed,andafixedimageiscalledaninterferencepattern.Thatistosay,foracertainplaceinspace,thetotalluminousintensityafterinterferencesuperpositionisnotnecessarilyequaltothesuperpositionoftheluminousintensityofthesub-beams,butmaybegreaterthan,equaltoorlessthantheluminousintensityofthesub-beams,whichisdeterminedbytheprincipleofwavesuperposition(Thatis,thesumofthecrestandthecrestistwicethecrest).
②Usuallyindependentlightsourcesareirrelevant.Thisisbecausetheradiationoflightisgenerallygeneratedbytheatoms'outerelectrons,whichautomaticallyreturntotheirnormalstate.Duetotheenergylossoftheradiatingatomandtheinteractionwiththesurroundingatoms,theradiationprocessofindividualatomsischaoticandofteninterrupted,andthecontinuousmatchingisveryshort.Eveninthecaseofextremelyraregasluminescence,theinteractionwiththesurroundingatomshasbeenReducedtotheweakest,andthedurationofasingleatomicradiationdoesnotexceed10^-8seconds.Whentheradiationofacertainatomisinterrupted,itwillre-radiateafterbeingexcited,butitwillhaveanewinitialphaseofrhyme.Thatistosay,thelightwaveofatomicradiationisnotacontinuousseriesofsimpleharmonicswhoseamplitudeandfrequencydonotchangewithtime,thatis,itisnotanidealmonochromaticlight,butremainsforashortperiodoftime(suchasτ=10-8s)Theamplitudeandfrequencyareapproximatelyunchanged,andappearinspaceasasequenceofsimpleharmonicsoffinitelength.Inaddition,thereisnocertainrulebetweentheinitialphasesofthelightwavetrainsofdifferentatomicradiation.Thetotalityoftheseintermittent,longorshortwavetrainswithirregularinitialphasesconstitutesamacroscopiclightwave.Duetothecomplexityofatomicradiation,theinterferencepatternssuperimposedatdifferentinstantsreplaceeachothersoquicklyandsoirregularlythattheusualdetectioninstrumentscannotdetectthisshort-terminterferencephenomenon.
Althoughthelightemittedbydifferentatomsorthelightemittedbythesameatomatdifferentmomentsisnotcoherent,theactuallightinterferencedoesnothavesuchharshrequirementsonthelightsource.ThelinearityofthelightsourceismuchhigherthanThelinearityofatomsandeventhewavelengthoflightaremuchlarger,andcoherentlightisnotemittedatthesametime.Thisisbecausetheactualinterferencephenomenonisthemacroscopicstatisticalaverageresultofalargenumberofatomsemittinglight.Fromamicroscopicpointofview,photonscanonlyinterferewiththemselves,anddifferentphotonsareincoherent;however,themacroscopicinterferencephenomenonisthatalargenumberofphotonsinterferewitheachother.Thestatisticalaverageeffectoftheresult.
③Duetotheadventoflasersinthe1960s,thecoherenceofthelightsourcehasbeengreatlyimproved.Atthesametime,theemergenceoffastphotoelectricdetectioninstrumentsshortensthetimeresponseconstantofthedetectioninstruments,sothattwoindependentlightsourcescanbeobserved.Interferencephenomenon.Inaddition,inhighschooltextbooks,therearealreadylightinterferenceexperiments,usinglasersorthesamelightbulbtoconductexperimentsthroughdoubleslits).
In1963,MagyaandManderusedavariabletubewithatimeconstantof10^-8~10^-9secondstophotographtheinterferencefringesoflasersemittedbytwoindependentrubylasers.Thereare23interferencefringesthatcanbevisuallydistinguished.
④Theacquisitionofcoherentlight.Forordinarylightsources,ensuringaconstantphasedifferencebecomesthekeytoachievinginterference.Inordertosolvethecontradictionbetweentheirregularandrapidchangeoftheinitialphaseintheluminescencemechanismandtheformationofinterferencefringesrequiringaconstantphasedifference,thelightwavesemittedbythesameatomcanbedecomposedintotwoorseveralcolumns,sothateachsub-beampassesthroughadifferentopticalpath.Thenmeet.Inthisway,althoughtheinitialphaseoftheoriginallightsourcechangesfrequently,theremaystillbeaconstantphasedifferencebetweenthesub-beams,andthereforeinterferencemayalsooccur.
⑤Thephenomenonoflightinterferenceisthemostdirectandpowerfulexperimentalevidenceofthewavenatureoflight.ThephenomenonoflightinterferencecannotbeexplainedbytheNewtonianparticlemodelatall,anditcanonlybeexplainedsatisfactorilywiththewavetheory.AccordingtotheNewtonianparticlemodel,thenumberofparticlesinthetwobeamsoflightshouldbeequaltothesumoftheparticlesineachbeam,butthephenomenonoflightinterferenceshouldexplainthatthenumberofparticleshaschanged,andthenumberofparticlesintheinterferencephaseismoredistributed;theinterferenceiscanceled.,Thenumberofparticlesislessthanthatofasinglebeamoflight,orevenzero.Theseproblemsaredifficulttoexplainbytheparticlemodel.Lookingattheinterferencephenomenonoflightfromanotherangle,itisalsoapowerfulnegationoftheparticlemodeloflight.Becauselightalwaystravelsinvacuumataspeedof3×10^8m/s,artificialmethodscannotbeusedtomakeanychangestothespeedoflight(unlessthespeedoflightisdifferentindifferentmedia.Butforagivenmedium,Thespeedoflightisalsocertain).Nolightpassesthroughthepointofinterferencecancellation.ThenaccordingtotheNewtonianparticlemodel,theparticlesshouldalwaysmoveinastraightlineataspeedof3×10^8m/s.Wheredotheselightparticlesgowheretheinterferencecancels?Iftwostreamsofparticlesmeetatthesepoints,Stoppedduetocollision,thenstopped(thatis,thespeedisnolonger3×10^8m/s,butbecomeszero)whatisthelightparticle?IfitismovedtotheplacewheretheinterferenceisconstructiveSo,whatforcemadeitexactlytomovethere?AllthesequestionsaresimplyunabletoanswertheNewtonianparticlemodel.However,thewavetheorycanexplainitconvincingly,andthepositionoftheinterferenceconstructiveanddestructiveandthefunctionalanalyticalformulaofthelightintensitydistributionoftheinterferencepatterncanbederivedquantitativelybysuperimposingthewavesinacertainphaserelationshipinspace.
Therefore,theinterferencephenomenonistheinevitableresultofthecoherentsuperpositionofwaves.Itundoubtedlyaffirmsthevolatilityoflight.Wecanfurtherextendittootherphenomena.Theoccurrenceofacertaindistributionofinterferencepatternscanbeusedasthemostreliableandpowerfulexperimentalevidencethatthephenomenonhasafluctuatingnature.
