Le même algorithme pour le code de redondance en anneau est vérifié.
S'il y a une erreur, elle doit être retransmise.
2. Exemples de génération de code de redondance cyclique et de vérification de l'exactitude des mots de code.
Analyse de l'algorithme du code de contrôle CRC La méthode de codage du code de contrôle CRC consiste à diviser les données binaires t(x) à envoyer par le polynôme générateur g(x), et à utiliser le reste final comme code de contrôle CRC.
Les étapes de mise en œuvre sont les suivantes :
(1) Supposons que le bloc de données à envoyer soit un polynôme binaire à m bits t(x), et (2) que le polynôme générateur soit un ordre r g(x). Ajouter
à la fin du bloc de données en ajoutant r zéros, (3) la longueur du bloc de données est augmentée à m+r bits, et (4) le polynôme binaire correspondant est.
(5) Divisez avec le polynôme générateur g(x), (6) Trouvez le reste comme polynôme binaire y(x) d'ordre r-1. Ce polynôme binaire y(x
) est le code de contrôle CRC de t(x) codé par le polynôme générateur g(x).
(7) Soustraire y(x) par modulo 2, et (8) obtenir un polynôme binaire. C'est la chaîne à envoyer qui contient le code de contrôle CRC.
Comme le montrent les règles de codage CRC, le codage CRC convertit en fait le polynôme binaire à m bits t(x) envoyé au nom de la génération pour qu'il soit divisible par g(x)
Est un polynôme binaire avec m+r bits, de sorte que les données reçues peuvent être utilisées pour supprimer g(x) lors du décodage. Si le reste est nul, cela signifie qu'il n'y a pas d'erreur dans le processus de transmission.
Si le reste n'est pas nul, alors il doit y avoir une erreur dans le processus de transmission. De nombreux circuits de décodage matériel CRC effectuent une détection d'erreur de cette manière.
Dans le même temps, il peut être considéré comme une combinaison de t(x) et de code de contrôle CRC, donc lors du décodage des données binaires reçues, supprimez les données r-bit de queue pour obtenir
Ce sont les données d'origine.
Afin de mieux comprendre le processus de codage du code de contrôle CRC, un exemple simple est utilisé ci-dessous pour illustrer le processus de codage du code de contrôle CRC. Parce que le processus de codage du CRC-32,
CRC-16, CCITT et CRC-4 sont fondamentalement les mêmes, seul le nombre de bits est différent du polynôme générateur.
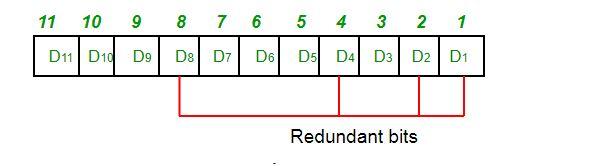
Bit redondant-le principe de fonctionnement du code de redondance cyclique Le code de redondance cyclique CRC peut être obtenu en utilisant le polynôme générateur pré-désigné G(X) lors du codage à l'extrémité émettrice et de la vérification à l'extrémité réceptrice, K Le bit d'information à envoyer
peut correspondre à un (k-1)
polynôme de degré K(X), et le bit redondant à r bits correspond à un (r-1) polynôme de degré R(X), n=k+r bits le mot de code composé de bits redondants à r bits correspond à un
(n-1)-degré polynôme T(X)=Xr*K (X)+R(X).
.Caractéristiques du code de contrôle de redondance cyclique
1) Toutes les erreurs de bits impairs peuvent être détectées ;
2) Toutes les erreurs double bit peuvent être détectées ;
3) Toutes les erreurs de salve inférieures ou égales à la longueur du bit de contrôle peuvent être détectées.
