Introductionauphénomène
Thelightintensitydistributiongeneratedwhenseverallightwaves (memberwaves) meetisnotequaltothesumofthelightintensitydistributioncausedbyeachmemberwavealone, butaphenomenonoflightanddarkphasesappears..Forexample, inYoung'sdoubleholeinterference (seeYoung'sinterferenceexperiment), thewaveletfromeachsmallholeH1orH2isamemberwave.Whentheholeisverysmall, thelightintensitycausedbythememberwavefromholeH1aloneThedistributionI1 (x) isroughlyuniforminarelativelylargerange; thesameistrueforthelightintensitydistributionI2 (x) causedbythememberwavescomingoutoftheholeH2alone.Thesumofthetwoisstillroughlyevenlydistributed.ThelightintensitydistributionI (x) causedbythetwomemberwavestogetherhasasignificantchangeinbrightnessanddarknesswithpositionx, whichisobviouslynotequaltoI1 (x) + l2 (X).
Chaque onde membre crée à elle seule une distribution d'intensité lumineuse à peu près uniforme, qui équivaut à ne nécessiter aucune diffraction évidente de chaque onde membre elle-même, car la diffraction provoquera également des franges lumineuses et sombres (voir diffraction lumineuse).
Il est à noter que l'intensité lumineuse mentionnée ci-dessus n'est pas la valeur instantanée de l'intensité du champ lumineux (proportionnelle au carré de l'amplitude), mais la valeur moyenne ou intégrée de l'intensité du champ lumineux dans une certaine période de temps t ; La longueur t dépend des performances du moyen de détection.
Le phénomène d'interférence se manifeste généralement sous la forme d'une répartition claire et sombre assez stable de l'intensité du champ lumineux dans l'espace ; il se manifeste parfois comme lorsqu'un certain paramètre du dispositif d'interférence change avec le temps, en recevant un point fixe. L'intensité lumineuse reçue change en alternance selon une certaine règle.
Thediscoveryoflightinterferencehasplayedanindelibleroleintheevolutionofthetheoryoflightwavesfromlightparticlestolightwavesinhistory.In1801, T.Yangproposedtheprincipleofinterferenceandfirstmadeadouble-slitinterferenceexperiment.Atthesametime, healsoexplainedthecolorformedbythefilm.In1811, DFJAragofirststudiedtheinterferencephenomenonofpolarizedlight.Inmoderntimes, lightinterferencehasbeenwidelyusedinmanyfieldssuchasprecisionmetrology, astronomicalobservation, photoelasticstressanalysis, andautomaticcontrolinopticalprecisionmachining.
Conditions de production
Aperçu
Seules deux sources lumineuses cohérentes avec la même fréquence, un déphasage constant et la même direction de vibration peuvent produire des interférences lumineuses.
Méthode spécifique
,therequirementsare:①Thefrequencyofeachmemberwave (thereforethewavelength )isthesame;②TheinitialphasedifferenceofanytwomemberwavesremainsunchangedwithinΔ .Condition②meansthatseverallightsourcesthatusuallyemitlightindependently,eveniftheyemitlightofthesamefrequency,therewillbenointerferencewhentheselightsmeet.Thereasonis:usuallythelightemittedbythelightsourceisalargenumberofwavetrainsrandomlydistributedintheinitialphase,andthedurationofeachwavetraindoesnotexceedtheorderof10seconds,thatis,every10secondsorso,theinitialphaseofthewavemustbeArandomchange.Moreover,theinitialphasesofthewavetrainsemittedbyanytwoindependentlightsourcesarestatisticallyirrelevant.Itcanbeimaginedthatwhenthewavesemittedbytheseindependentlightsourcesmeet,adefinitepatternoffringesisonlyproducedinaveryshorttime,andevery10secondsorso,itisreplacedwithanotherpattern.Sofar,therehasbeennodetection.Ortherecordingdevice InordertomakethelightintensitydistributionofthesyntheticwavefieldstablewithinaperiodoftimeintervalΔ therequirementsare: ①Thefrequencyofeachmemberwave (thereforethewavelength isthesame; ②TheinitialphasedifferenceofanytwomemberwavesremainsunchangedwithinΔ .Condition②meansthatseverallightsourcesthatusuallyemitlightindependently, eveniftheyemitlightofthesamefrequency, therewillbenointerferencewhentheselightsmeet.Thereasonis: usuallythelightemittedbythelightsourceisalargenumberofwavetrainsrandomlydistributedintheinitialphase, andthedurationofeachwavetraindoesnotexceedtheorderof10seconds, thatis, every10secondsorso, theinitialphaseofthewavemustbeArandomchange.Moreover, theinitialphasesofthewavetrainsemittedbyanytwoindependentlightsourcesarestatisticallyirrelevant.Itcanbeimaginedthatwhenthewavesemittedbytheseindependentlightsourcesmeet, adefinitepatternoffringesisonlyproducedinaveryshorttime, andevery10secondsorso, itisreplacedwithanotherpattern.Sofar, therehasbeennodetection. Oul'appareil d'enregistrement shorterthan10secondsisused(suchadevicecanbedone),thelightwavesemittedbytwoindependentlasersofthesamefrequencywillbeInterferencecanalsobeobserved.Inaddition,takingthedouble-waveinterferenceasanexample,itisalsorequired:③Theamplitudeofthetwowavesmustnotbeverydifferent;④Thepolarizationplanesofthetwowavesmustberoughlythesameatthesuperpositionpoint. cankeepupwithsuchasharpchange, sowhatisobservedistheaverageeffectoftheabove-mentionedlargenumberofpatterns, thatis, auniformlightintensitydistributionratherthanastreakoflightanddark.However, modernspeciallasershavebeenabletoemitwavetrainsaslongastensofkilometers, thatis, thewavetraindurationisontheorderof10seconds.Therefore, itcanbesaidthatifadetectorwithatimeresolutionΔ shorterthan10secondsisused (suchadevicecanbedone), thelightwavesemittedbytwoindependentlasersofthesamefrequencywillbeInterferencecanalsobeobserved.Inaddition, takingthedouble-waveinterferenceasanexample, itisalsorequired: ③Theamplitudeofthetwowavesmustnotbeverydifferent; ④Thepolarizationplanesofthetwowavesmustberoughlythesameatthesuperpositionpoint.
Whenthecondition③isnotsatisfied, althoughinterferencefringescanstillbeproducedinprinciple, thedifferencebetweenthelightanddarkofthefringesisverysmall, andtheinterferencephenomenonisnotobvious.Condition④Therequirementisnecessarybecausewhenthepolarizationplanesoftwolightwavesareperpendiculartoeachother, regardlessofthefixedphasedifferencebetweenthetwolightwaves, thelightintensityofthecombinedfieldisthesamevalue, andtherewillbenoalternatinglightanddark (toobserveAlternatelightanddark, withthehelpofpolarizingelements).
Les quatre points ci-dessus sont généralement désignés comme des conditions de cohérence.
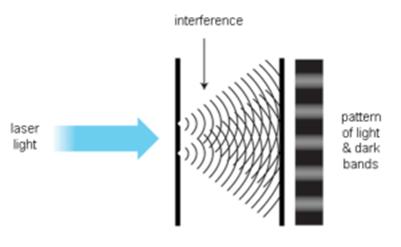
Générer des ondes lumineuses cohérentes
Aperçu
Thewaytoobtainasetofcoherentlightwavesfromagenerallightsourceistocombinealightsourcewithacertainopticaldevice (interferencedevice) Theemittedlightwave (sourcewave) isdividedintoseveralwaves.Sincethesewavescomefromthesamesourcewave, whentheinitialphaseofthesourcewavechanges, theinitialphaseofeachmemberwavechangesaccordingly, sothatthephasedifferencebetweenthemremainsunchanged.Atthesametime, thepolarizationdirectionofeachmemberwaveisalsoconsistentwiththesourcewave, sotheirpolarizationdirectionsarealsoroughlythesameatthepointofinvestigation.Thegeneralinterferencedevicecanmaketheamplitudeofeachmemberwavenottoogreat.Therefore, whenthelightsourceemitslightofasinglefrequency, alltheabovefourconditionscanbemet, andinterferencephenomenonoccurs.Whenthelightsourceemitsmanyfrequencycomponents, eachsingle-frequencycomponent (correspondingtoacertaincolor) willproduceacorrespondingsetoffringes, andwhenthesefringesoverlap, theywillappearascoloredfringes.
Voici un complément à la méthode de Thomas Young pour obtenir une lumière cohérente à l'époque : en ajoutant un petit trou S avant le double trou, selon le principe de Huygen, la lumière diffractée par le petit trou S devient une onde asphérique, ainsi obtient une lumière cohérente.
La méthode du front d'onde partiel
Thepartialwavefrontmethod.Dividethewavefrontofthepointlightsourceintotwoparts, makethempassthroughtwoopticaltoolgroups, andoverlapafterbeingreflected, refractedordiffractedtoforminterferenceinacertainarea.Sinceanypartofthewavefrontcanberegardedasanewlightsource, andeachpartofthesamewavefronthasthesamephase, theseseparatedpartsofthewavefrontcanbeusedaslightsourceswiththesameinitialphase, regardlessofthephasechangeofthepointlightsourceHowfast, theinitialphasedifferenceoftheselightsourcesisconstant.Young'sdoubleslits, Fresneldouble-sidedmirrors, andLoemirrorsareallsuchwavedivisionfrontinterferencedevices.
Méthode de sous-amplitude
Sous-amplitudemethod.Whenabeamoflightisprojectedontheinterfacebetweentwotransparentmedia, partofthelightenergyisreflectedandtheotherpartisrefracted.Thismethodiscalledthesub-amplitudemethod.Thesimplestamplitude-dividedinterferencedeviceisathinfilm, whichusestheupperandlowersurfacesofthetransparentfilmtosequentiallyreflectincidentlight, andtheinterferencephenomenonformedbytheencounterofthesereflectedlightwavesinspace.Sincethereflectedlightontheupperandlowersurfacesofthefilmcomesfromtwopartsofthesameincidentlight, theyonlyexperiencedifferentpathsandhaveaconstantphasedifference, sotheyarecoherentlight.Anotherimportantsub-amplitudeinterferencedeviceistheMichelsoninterferometer.
Franges d'interférence
Parmitoutestypesdefrangesd'interférence,lesfrangesd'interférenced'égaleinclinaisonetd'égaleépaisseursontdeuxtypiques.
Classification des interférences
Doublelightwaveinterference
Il s'agit de l'interférence de deux ondes membres. L'interférence à double trou et à double fente de Young, l'interférence à double miroir de Fresnel impliquant des anneaux de Newton, etc. appartiennent à cette catégorie.
Interférence multi-ondes
Theinterferenceofmorethantwomemberwaves.Lumo-Gerkefilminterferencefallsintothiscategory.InFigure1, AisaparallelplateglasswithaninclinedincidentwindowBCatoneend.ThesourcewaveemittedfromSenterstheglasssheetthroughBCandisreflectedmultipletimesbetweenitsupperandlowersurfaces.Everytimeitreflectsontheuppersurface, awaveisrefractedintotheairatthesametime.Allwavesthatarerefractedintotheaireachtimeareagroupofmemberwavescausedbythesamesourcewaveinawayofsub-amplitude.ObservetheinterferencefringesonthefocalplaneΠofthelensL.ThephasedifferencebetweentwoadjacentwavesatpointPis: whereλisthewavelengthofthelightwaveinvacuum, nistherefractiveindexoftheglass, tisthethicknessoftheglasssheet, andβisthedifferencebetweentheopticalpathauxiliarylineintheglasssheetandthesurfacenormalAngle.Thefringesofthelightintensitydistributiononthereceivingsurfaceareveryfineandsharp, whichisacharacteristicofmulti-waveinterference.
Interférence de la lumière polarisée
Dans les interférences mentionnées ci-dessus, chaque onde membre peut être considérée comme ayant la même direction de polarisation au point d'inspection.
Application
Accordingtotheprincipleoflightinterference, thelengthcanbepreciselymeasured.Forexample, useMichelsoninterferometertocalibratethelengthoftheblockgauge.Themethodisasfollows.Usealaserbeamwithgoodmonochromaticity (wavelengthλ) asthelightsource, andinstallaprecisecontactonthemovablearmoftheMichelsoninterferometer, firstmakethecontactcontactoneendoftheblockgauge, Thenremovetheblockruleandmakethemovablemirrormove.Atthistime, everytimeyoumoveλ / 2, theopticalpathdifferenceinthetwoarmsincreasesbyλ, sothatthedetectorplacedinthecenteroftheinterferencefieldofviewoutputsachangeinstrength, increasingthenumberofthecounterby1.Untilthecontactcontactsthebasesurface (theotherendoftheblockgaugewasoriginallyplacedonthebasesurface) .Ifthetotalnumberofcountersaddedisn, thelengthoftheblockgaugeismeasured.
L'appareil précis peut mesurer avec précision à moins de ± 0,1, de sorte que l'erreur de mesure de la longueur ne dépasse pas ± λ/20.
Usinginterferencephenomenoncanalsodetecttheslightdifferencebetweenthegeometryoftheworkpiecesurfaceandthedesignrequirementsduringthemachiningprocess.Forexample, ifyouwanttoprocessaplane, youcanfirstuseprecisiontechnologytomanufactureaplaneglassplate (modèle) withhighprecision.Theplaneofthetemplateisbroughtintocontactwiththesurfaceoftheparttobetested, soanairfilmisformedbetweenthetwosurfaces.Ifthesurfacetobemeasuredisindeedagoodplane, theairfilmisofequalthicknesseverywhereoraregularwedgeshape.Whenlightisirradiated, theinterferencelightintensityformedbythethinfilmisapieceofuniformorparallelandevenlyspacedstraightstripes.Ifthesurfacetobemeasureddeviatesfromtheplaneinsomeareas, theintensityoftheinterferencelighthereisdifferentfromelsewhereortheinterferencefringesappeartobecurvedthere.Fromthefringevariation, itcanbeinferredthatthesurfacetobemeasureddeviatesfromtheplane.Itiseasytoobservethatthedeviationisafractionofthewavelength.
La description
①Iftheintensityofeachplaceintheoverlappingareaisnotexactlythesame, acertainintensitydistributionisformed, andafixedimageiscalledaninterferencepattern.Thatistosay, foracertainplaceinspace, thetotalluminousintensityafterinterferencesuperpositionisnotnecessarilyequaltothesuperpositionoftheluminousintensityofthesub-faisceaux, butmaybegreaterthan, equaltoorlessthantheluminousintensityofthesub-faisceaux, whichisdeterminedbytheprincipleofwavesuperposition (thatis, thesumofthecrestandthecrestistwicethecrest).
②Usuallyindependentlightsourcesareirrelevant.Thisisbecausetheradiationoflightisgenerallygeneratedbytheatoms'outerelectrons, whichautomaticallyreturntotheirnormalstate.Duetotheenergylossoftheradiatingatomandtheinteractionwiththesurroundingatoms, theradiationprocessofindividualatomsischaoticandofteninterrupted, andthecontinuousmatchingisveryshort.Eveninthecaseofextremelyraregasluminescence, theinteractionwiththesurroundingatomshasbeenReducedtotheweakest, andthedurationofasingleatomicradiationdoesnotexceed10 ^ -8seconds.Whentheradiationofacertainatomisinterrupted, itwillre-radiateafterbeingexcited, butitwillhaveanewinitialphaseofrhyme.Thatistosay, thelightwaveofatomicradiationisnotacontinuousseriesofsimpleharmonicswhoseamplitudeandfrequencydonotchangewithtime, thatis, itisnotanidealmonochromaticlight, butremainsforashortperiodoftime (suchasτ = 10-8s) Theamplitudeandfrequencyareapproximatelyunchanged, andappearinspaceasasequenceofsimpleharmonicsoffinitelength .En outre,il n'y a pas de règle certaine entre le phasesdestrainsd'ondes lumineusesdedifférentsrayonnementsatomiques.Latotalitédecestrainsd'ondesintermittentes,longuesoucourtesavecdesphasesinitialesirrégulièresconstituentuneondelumièremacroscopique.En raison delacomplexitédurayonnementatomique,lesmodèlesd'interférencesuperposésàdesinstantsdifférentsseremplacentsirapidementetsoirrégulièrementquelesphénomènesdedétectionnonusuelsnepeuventpasdétecter.
Althoughthelightemittedbydifferentatomsorthelightemittedbythesameatomatdifferentmomentsisnotcoherent, theactuallightinterferencedoesnothavesuchharshrequirementsonthelightsource.ThelinearityofthelightsourceismuchhigherthanThelinearityofatomsandeventhewavelengthoflightaremuchlarger, andcoherentlightisnotemittedatthesametime.Thisisbecausetheactualinterferencephenomenonisthemacroscopicstatisticalaverageresultofalargenumberofatomsemittinglight.Fromamicroscopicpointofview, photonscanonlyinterferewiththemselves, anddifferentphotonsareincoherent, mais themacroscopicinterferencephenomenonisthatalargenumberofphotonsinterferewitheachother.Thestatisticalaverageeffectoftheresult.
③Duetàtêteventoflasersdanslesannées60,lacohérencedelasourcelumineuseaétéfortementaméliorée.En même temps,l'émergenced'instrumentsdedétectionphotoélectriquerapideréduitletempsderéponseconstantdesinstrumentsdedétection,de sorte quedeuxsourceslumièreindépendantespeuventêtreobservées.
En 1963, Magya et Mander ont utilisé un tube variable avec une constante de temps de 10^-8~10^-9 secondes pour photographier les franges d'interférences des lasers émis par deux lasers rubis indépendants. Il existe 23 franges d'interférences qui peuvent être distinguées visuellement.
④Theacquisitionofcoherentlight.Forordinarylightsources, ensuringaconstantphasedifferencebecomesthekeytoachievinginterference.Inordertosolvethecontradictionbetweentheirregularandrapidchangeoftheinitialphaseintheluminescencemechanismandtheformationofinterferencefringesrequiringaconstantphasedifference, thelightwavesemittedbythesameatomcanbedecomposedintotwoorseveralcolumns, sothateachsub-beampassesthroughadifferentopticalpath.Thenmeet.Inthisway, althoughtheinitialphaseoftheoriginallightsourcechangesfrequently, theremaystillbeaconstantphasedifferencebetweenthesub-faisceaux, andthereforeinterferencemayalsooccur.
⑤Thephenomenonoflightinterferenceisthemostdirectandpowerfulexperimentalevidenceofthewavenatureoflight.ThephenomenonoflightinterferencecannotbeexplainedbytheNewtonianparticlemodelatall, anditcanonlybeexplainedsatisfactorilywiththewavetheory.AccordingtotheNewtonianparticlemodel, thenumberofparticlesinthetwobeamsoflightshouldbeequaltothesumoftheparticlesineachbeam, butthephenomenonoflightinterferenceshouldexplainthatthenumberofparticleshaschanged, andthenumberofparticlesintheinterferencephaseismoredistributed; theinterferenceiscanceled, Thenumberofparticlesislessthanthatofasinglebeamoflight, orevenzero.Theseproblemsaredifficulttoexplainbytheparticlemodel.Lookingattheinterferencephenomenonoflightfromanotherangle, itisalsoapowerfulnegationoftheparticlemodeloflight.Becauselightalwaystravelsinvacuumataspeedof3 × 10 ^ 8 m / s, artificialmethodscannotbeusedtomakeanychangestothespeedoflight (unlessthespeedoflightisdifferentindifferentmedia.Butforagivenmedium, Thespeedoflightisalsocertain) .Nolightpassesthroughthe. pointofinterferencecancellation.ThenaccordingtotheNewtonianparticlemodel, theparticlesshouldalwaysmoveinastraightlineataspeedof3 × 10 ^ 8 m / s.Wheredotheselightparticlesgowheretheinterferencecancels? Iftwostreamsofparticlesmeetatthesepoints, Stoppedduetocollision, thenstopped (thatis, thespeedisnolonger3 × 10 ^ 8 m / s, butbecomeszero) whatisthelightparticle? IfitismovedtotheplacewheretheinterferenceisconstructiveSo, whatforcemadeitexactlytomovethere? AllthesequestionsaresimplyunabletoanswertheNewtonianparticlemodel.However, thewavetheorycanexplainitconvincingly, andthepositionoftheinterferenceconstructiveanddestructiveandthefunctionalanalyticalformulaofthelightintensitydistributionoftheinterferencepatterncanbederivedquantitativelybysuperimposingthewavesinacertainphaserelationshipinspace.
Par conséquent, le phénomène d'interférence est le résultat inévitable de la superposition cohérente des ondes. Il affirme sans aucun doute la volatilité de la lumière. Nous pouvons encore l'étendre à d'autres phénomènes.
