Définition de base
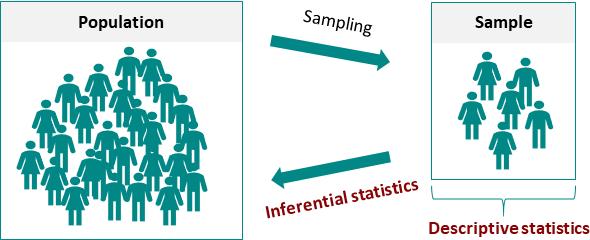
Les statistiques inférentielles consistent en des nombres de probabilité pour déterminer la possibilité d'une certaine relation entre deux (ou plusieurs groupes) de nombres, et pour déduire des caractéristiques globales à partir d'échantillons de caractéristiques.
La recherche scientifique en éducation est généralement impossible d'examiner un par un tous les objets à étudier, mais de prélever un certain échantillon dans l'ensemble pour la recherche. Par exemple, pour comprendre les caractéristiques démographiques d'une région, il est impossible de mesurer les caractéristiques de chaque personne.
Dans la conception de la recherche, les sujets sont souvent divisés en différents groupes en fonction de certaines exigences pour faciliter la recherche et le traitement statistique, de sorte que des problèmes tels que l'estimation de la population à partir de l'échantillon et la déduction de la population se posent.
Parexemple, tounderstandthedemographiccharacteristicsofanarea, itisimpossibletomeasurethecharacteristicsofeachpersononebyone, andtoinspectthequalityoffinishedproducts, whichisoftendestructive, anditisimpossibletoinspecteachproduct..Thisrequiressamplingindividualsamplesformeasurement, andinferringtheoverallcharacteristicsbasedontheobtaineddata.Thisistheproblemthatinferencestatisticsmustsolve.Inferentialstatisticsisveryusefulbecauseitallowsustogivelimitedinformation (échantillons) todrawconclusionsaboutthepopulation.
Étape
Test d'hypothèse : hypothèse nulle et hypothèse opposée ; test unilatéral et test bilatéral.
Inspection unilatérale et inspection bilatérale ;
calcul d'erreur d'échantillonnage ;
Prise de décision en valeur P ;
Calcul de la taille d'effet.
Contenu principal
Les statistiques déduites comprennent deux aspects : l'estimation globale des paramètres et la formulation d'hypothèses.
Estimation globale des paramètres
Lorsqu'un ensemble de données est obtenu à partir d'un échantillon dans la recherche, comment utiliser cet ensemble d'informations pour estimer les caractéristiques globales, c'est-à-dire comment déduire la situation globale à partir des résultats locaux, appelée estimation globale des paramètres. L'estimation globale des paramètres peut être divisée en estimation ponctuelle et estimation par intervalle.
Pointestimationistousesamplestatisticstoestimatetheoverallparameters, becausethesamplestatisticsarethevalueofacertainpointonthenumberaxis, andtheestimatedresultisalsorepresentedbythevalueofapoint.Sincethisestimateisasinglevalue, thereisalwaysanerror, andtheerrorcannotbeaccuratelycalculated.Inaddition, thepointestimatecannotindicatetheprobabilityofgivingacorrectestimateoftheoverallparameter.Therefore, thispointestimatecanonlybeusedasanimpreciseroughestimate, andabetterwayistoestimatetheoverallparametersinaninterval.
L'estimation de l'intervalle est basée sur des statistiques d'échantillonnage, en utilisant le principe de la distribution d'échantillonnage et en utilisant la probabilité pour indiquer que le paramètre global peut tomber dans un certain intervalle numérique.
Tests d'hypothèses
Danslesstatistiques,desconclusionsgénéralessonttiréesdesdifférencesd'unéchantillondestatistiquespourdéterminers'ily a ou non desdifférencesentrelesparamètresglobaux.Ceprocessusd'inférenceestappelétestd'hypothèse.
Silarépartitiondelapopulationestconnuelorsquel'hypothèseesteffectuée,ilestnécessaired'effectuerunehypothèsesurleparamètredelocalisationdelapopulation,appeléetestd'hypothèseparamétrique.
Analyse comparative
Theconfrontationaldebatebetweenthedescriptiveandinferentialschoolsinstatisticsinthe1920sand1940scanbasicallybesaidtobetherapiddevelopmentofstatisticalinferenceideas.Andit'sover.Butinthe1960s, withtheriseofBayesianstatisticalthinking, peoplewentbacktounderstandthewholestatisticsandvariousideasinitfromamoreobjectiveperspective, andtriedtofindthebasisofvariousstatisticalideas.Theexistenceofstatisticalknowledgeobjectsandmethodsthathavethesamefundamentalsignificanceiswhatwecallthegenerallawandprobabilitytheory.Thesetwopointshavebecomethemostessentialthingsthatvariouswesternstatisticalschoolsofthoughtadhereto, andtheyarethetwocoresoftheentirestatistics.However, ce "générique" statisticalviewisstillbasedonthesignificantdifferencesbetweenvariousstatisticalschoolsofthought.Asfarasdescriptivestatisticsandinferentialstatisticsareconcerned, thisdifferenceismainlyreflectedinthefollowingthreeaspects:
Firstofall, differentthinkingandunderstanding.Descriptivestatisticsbelievesthatonlyalargenumberofobservations (notafewexperiments) canfullyandcorrectlyreflecttheregularityofappearancechanges, andifthisobservationislimitedtoafewsmall, partialexperiments, theconclusioncanbedrawnItmustbeone-sidedorevenwrong.Fromaphilosophicalpointofview, itadherestothetheoryofknowability, opposesthetheoryoflimitedhumanintelligence, andbelievesthathumanbeingsarefullycapableofmakingalargenumberofevencomprehensiveobservations.Onthecontrary, inferentialstatisticsstronglyopposetheextensiveandcomprehensivecollectionoflargeandcomplexrawdata, thinkingthatinsteadofthis, itisbettertofocusonexperimentsthatarepreciselydesignedandcontrolled.Thedatacanbetrulydescribedasinformativeandreliable, andthuscanitmoreaccuratelyreflecttheregularityofchangesinthephenomenon.
En second lieu, theapproachisdifferent.Thisisexactlythedifferencethatisinevitablyderivedfromthedifferenceinthinkingandunderstanding.Descriptivestatisticsinsistonalargenumberofobservations, whileinferentialstatisticsinsistonsampleanalysis, anditsessenceissmallsampleanalysis.Therefore, itcanberoughlysaid:. Thelawofdescriptivestatisticsisdisplayed "directement" intheoverallinformation (comprehensivedata) andisdescribed (condensé); whilethelawofinferringstatisticsisthroughsampleinformation (de partialdata)) Whatappears "indirectement" isinferred (estimatedortested).
Enfin, thelogicalstructureisdifferent.Inferentialstatisticsadvocatesusingsamplestomakeinferences.Therefore, itmustfirstconstructthetwomostbasicstatisticalcategories, namelythepopulationandthesample.Otherstatisticalcategoriesorconceptsarerelativelyderivedfromtheirinferiorcategoriesorconcepts.Callitasubcategoryorsubconcept.Incontrast, fordescriptivestatistics, thisisnotindispensableforthebasiccategory (especiallythelatter) .Ifyouwanttousethispairofbasiccategoriestoestablishtheentirestatisticalcategoryorconceptualsystem, youcanroughlysaythatdescriptivestatisticsbelongtolargesampleanalysis, whileinferentialstatisticsbelongtosmallsampleanalysis.
Application d'enseignement
Selectthecasethatisclosesttothestudent'slife, throughthedesignofpracticalteaching, letstudentsparticipateintheacquisitionofoveralldata, randomsampleextraction, calculationofcommonstatistics, Toinferandtesttheoverallparameters, graduallygainanintuitiveunderstandingofsomekeyissuesandconceptsinstatisticalinferencetheoriessuchassamplingdistribution, parameterestimation, andhypothesistesting.ThismethodcanvisualizeabstractstatisticaltheoriesandisbeneficialtoDeepenstudents'understandingofstatisticalinferencetheory.
